Die „vierbeinige“ Eintagsfliege des ARISTOTELES
Die „vierbeinige“ Eintagsfliege des ARISTOTELES von Michael Stelzner Inhaltsverzeichnis 1. Die Behauptung eines Phänomens und ihre Absicht Der große Denker ARISTOTELES lässt sich in seiner
Die Quadratur des Kreises und seine verborgene Bedeutung
von Michael Stelzner
Die Redewendung «Quadratur des Kreises» drückt aus, dass eine Aufgabe unlösbar ist. Ihr zugrunde liegt das unlösbare mathematische Problem, mit Zirkel und Lineal ein Quadrat mit demselben Flächeninhalt eines Kreises zu konstruieren. Lineal und Zirkel sind die zwei Instrumente, um die zwei sich in ihrer Art unterschiedenen Längenmaße, die gerade und die gebogene Linie zu bestimmen. Die Dimension der Fläche wird über diese zwei Linienarten geformt. Ihre gestalthaften Vertreter sind das Quadrat und der Kreis. Beide bilden über die für sie spezifischen Linien eine Fläche aus. Die Flächen aber sind nicht gänzlich miteinander in Einklang zu bringen, wie auch schon die ihnen zugrundeliegenden Linienarten sich wesentlich voneinander unterscheiden. Das Verhältnis zwischen der geraden und der gebogenen Linie, sowie das aus ihnen hervorgehende Verhältnis von Quadrat und Kreis entspricht dem Wesen der Zwei. Es ist «zwistig».
Dem Problem der Unmöglichkeit der Quadratur des Kreises liegt eine tieferliegende philosophische Frage zugrunde. Es ist die Frage, wie und warum kam es zur Existenz der Zwei? Wie und aus welchem Anlass heraus entstand aus der den Anfang bildenden Einheit, Ganzheit und Vollkommenheit überhaupt die Zwei und das Zweite?
Die derart gestellte Frage kann so nicht befriedigend beantwortet werden, weil schon die in unserer Vorstellung existierende Einheit und Ganzheit (1) von uns nicht vollständig erfasst werden kann. Sie bleibt immer ein Stückweit im Dunkeln. Der Zugriff auf sie ist nur mittelbar und nicht unmittelbar möglich. Um Sie zu verstehen, brauchen wir noch etwas Anderes als nur die Entitäten Eins und Zwei. Wie brauchen eine Hilfe, ein Drittes, das über das Wesen der zwei Entitäten hinausreicht. Dieses Dritte ist aber in einer ganz anderen Art «anders» als die Andersartigkeit zwischen den Entitäten Eins und Zwei, die wir beide aus einer linearlogischen Perspektive betrachten. Dieses Dritte ist von nichtlinearer Natur, analog dem dritten Punkt in einem Dreieck, der sich über die lineare Verbindung der ersten und zweiten Entität erhebt und so die Verbindung zwischen den Gegensätzen möglich werden lässt.
Jenes Verbindungselement das hier ein Drittes ist, ist aus der Sicht der ersten Dimension (1—2), der Dimension der Linien ein Anderes und somit «Zweites», denn es erhebt sich über sie und eröffnet darin die Dimension der Fläche (siehe Abb. 1). Die Existenz der zweiten und höheren Dimension (II) ist unabdingbar, um den Widerspruch zwischen der Eins und der Zwei zu (er)lösen. Das zu erkennen, ist der Schlüssel, um scheinbar unlösbare Widersprüche einer Lösung zuzuführen.
Mit dieser Erkenntnis wenden wir uns erneut die Frage zu, weshalb aus der Eins die zwei hervorgehen konnte und warum dies überhaupt nötig war? Diese grundsätzliche Frage formuliert die Philosophie in etwas komplizierterer Form, aber nicht weniger irritierend, wenn sie fragt: Warum existiert überhaupt etwas und nicht vielmehr Nichts?
Der Schlüssel zur Beantwortung verlangt eine Umkehr unserer Denkrichtung. Wenn wir zuvor festgestellt haben, dass ein Anderes (II) und Drittes (3) notwendig ist, um scheinbar unlösbare Widersprüche einer Lösung zuführen zu können, müssen wir bei unserem Denkvorgang dieses Andere (II), das aus der vorangehenden linearen und notwendig beschränkten Sicht ein Drittes (3) ist, nun auch hier voraussetzen. Das bedeutet, dass wir das Wesen der Zwei (2) aus einer anderen und höheren Perspektive (II) betrachten müssen. Aus ihr heraus wird das Zweite (2) zur Funktion (3). Wenn wir die Zweizahl in einem höheren Dritten wiedererkennen, werten wir ihr Wesen auf. Wir adeln die einst weniger geschätzte Zwei.
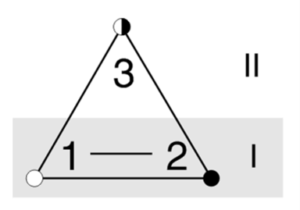
Abb. 1 Die Polarität 1—2 wird durch die 3 überwachsen. Die ist eine erhöhte Polarität (II).
Übertragen wir die Erkenntnis auf unsere Frage, warum aus der Eins die Zwei hervorgeht, so ist sie nur deshalb unlösbar, weil wir die Zwei nicht ihrem Wesen entsprechend aufwerten. Die Frage selbst erwächst aus diesem, unseren Mangel. Die Crux dieser Frage lag in der falschen, einseitigen Blickrichtung des Fragenden. Der Schlüssel zur Antwort des Verhältnisses der Zwei zur Eins findet sich in erster Linie in der Frage nach dem Wesen der Zwei und erst in zweiter Linie in der Frage nach dem Wesen und der Existenz der Eins. Die entscheidende (2) Frage findet ihre Antwort in der Selbstbestimmung der Zwei und die ist in Wirklichkeit die Frage nach der Funktion (3) der Zwei.
Wenden wir uns nach dem Gesagten nun erneut der Geometrie der Ebene zu, mit deren Hilfe wir den Kreis und das Quadrat vor unserem Auge erscheinen lassen. Die Hinwendung zu ihr ist der richtige Schritt, denn sie repräsentiert die zweite Dimension und ist insofern die geforderte Hinwendung zur Zwei. Die neue Perspektive wird uns zuvor unzugängliche Erkenntnisse möglich machen. Wir werden aber unseren analytischen Blick nicht nur auf Basis der Zwei in Form der Dimension der Fläche schärfen. Wir werden unseren Blick auch innerhalb dieser Dimension vom Standpunkt der Zwei aus entwickeln. Wir starten bei der Erstellung einer Gestalt nicht bei der Eins, sondern bei der Existenz der Zwei. Das bedeutet, wir schauen auf die Flächen, die von der Zahl Zwei getragen werden. Das ist in erster Linie das Quadrat mit der Fläche 2 (Abb. 2).
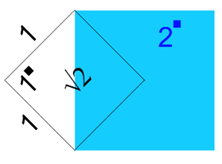
Abb. 2 Über die irrationale Seitenlänge (√2) des Quadrates mit der Fläche 2 lässt sich das Quadrat mit der Fläche 1 entwickeln.
Die Seitenlänge eines Quadrats vom Flächeninhalt 2 hat die Länge √2 und die ist zugleich die Diagonale eines Quadrats vom Flächeninhalt 1. Es ist die Qualität (der «Inhalt», die Fläche) der Zweizahl ( 2▪ ) über die man zu dem an sich verborgenen Wesen der Einheit und Ganzheit ( 1▪ ) gelangt, sofern man den irrationalen Teil ( √2 ) der Zweizahl würdigt. Anders ausgedrückt: Die Zuordnung der zwei sich ihrem Inhalt (Fläche) nach unterscheidenden Quadrate ( 2▪ → 1▪ ) wird über den Weg und die Existenz des wirklich Anderen – hier der √2 – möglich. Das Andere (II) wird «Wirklichkeit» im eigentlichen Wortsinn. Über sein Wirken entsteht das Quadrat mit dem bedeutsamen «Inhalt» der Fläche 1.
Wir sehen, dass die planimetrische Darstellung irrationaler Verhältnisse diese dem Verstand näher bringt und darin das Vermögen der Geometrie veranschaulicht. Die plane Geometrie macht über den rechten Umgang mit der Zweiheit etwas möglich, was mit dem gewöhnlichen Verstand nicht oder nur schwer zu erfassen ist. Jenes Vermögen der Geometrie veranlasste Platon in seinem letzten Buch «Epinomis» dazu, Kritik daran zu üben, sie nur als «Feldmesskunst» zu bezeichnen, wie es ihr Name eigentlich besagt. Die Kunst und Aufgabe der besonderen Wissenschaft bestehe vielmehr im «Ähnlichmachen¹ der Zahlen, die ihrer Natur nach unähnlich erscheinen», was «dank der Besonderheit der Flächen» möglich sei (Epinomis 990d).
In der Epinomis, dem sogenannten 13ten Buch der Gesetze illustriert Platon die darstellbare und fruchtbare Grenzüberschreitung vom Archetyp der Zwei zum Archetyp der Eins, mit Hilfe der Aufwertung des Wesens der Zwei (2) zu dem völlig Anderen (II). Über dieses Wissen erklärt sich ein besonderes Phänomen, das ebenso die Archetypen 1 und 2 in ihrem direkten Verhältnis zueinander anschaulich macht und das Thema der sogenannten «Quadratur des Kreises» erhellt:
Der Einheitskreis (r =1) umschließt das Quadrat der Fläche 2 (siehe Abb. 3 u. 4). Das Bild lässt die Archetypen Eins und Zwei, Kreis und Quadrat in ihrer gestalthaften Unterscheidung zueinander nicht nur bestehen, sondern zeigt zugleich ihre eindeutige Beziehung auf. Das Bild erfasst ihren Wesensunterschied. Die Eins ist im Kreis, dem Symbol für das Ganze die denkbar einfachste Größe (r =1) und zugleich der Parameter der Einheit und Ganzheit. Der Einheitskreis macht das vollkommene Sein ansichtig. Das von ihm umschlossene Quadrat der Fläche 2 hingegen repräsentiert die konkrete Form in ihrer polaren Existenz. Die «eindeutige» Beziehung der Figuren erzählt vom Gehalt und der Fülle im konkreten Dasein (4). In der Terminologie der Religion wird die Welt (Quadrat) von der Einheit, Ganzheit und Vollkommenheit (Kreis) gänzlich umschlossen, sprich geschützt und erhalten.
Die Botschaft dieses geometrischen Gleichnisses ist es, sowohl das Eins-Sein (1) als auch das Unterschieden-Sein (2) als unverwechselbare, sich ergänzende Archetypen anzuerkennen. Konkret bedeutet das, dass man sowohl die Nichtgreifbarkeit der Einheit (1) als auch den grundsätzlichen Bruch (2) der Dinge erkennen und akzeptieren muss. Nur beide zusammen machen den ewigen Fluss und Fortentwicklung (3) möglich.
Aus rein linearlogischer Sicht überschreitet die Kreis-Quadrat-Problematik den Glauben an die Verlässlichkeit der erlebbaren Dimensionen und ihrer Grenzen. Die Quadratur des Kreises scheitert und doch nähert man sich ihr mit mathematischen Raffinessen immer weiter an. Das ist paradox, befördert aber den technischen Fortschritt. In Wirklichkeit verbirgt sich hinter der Paradoxie die Begründung, warum die Quadratur des Kreises nicht möglich ist und gerade deshalb die Welt in ihrer Existenz erhält.
Im Mittelpunkt des Gleichnisses steht der Einheitskreis als Metapher für die Einheit, Ganzheit und Vollkommenheit. Er führt uns über die Geometrie zu zwei Aussagen, die ihrem Grunde nach religiöse Aussagen sind:
a) Die Einheit schließt die konkrete Polarität ein (Abb. rechts)
b) Die Welt schließt in ihrer archetypischen Form, der Vier die Einheit ein (Abb. links).
Abb. 3 Der Einheitskreis (r = 1) hat aus zweifacher Sicht ein eindeutig definiertes Verhältnis zur «Welt der Vier»
Die technische Unmöglichkeit der Quadratur des Kreises erzählt von der technischen Unmöglichkeit des Zusammenfindens von Rationalität und Irrationalität. Betrachten wir aber den Kreis als solchen, dann erleben wir es in ihm unmittelbar im Verhältnis seines Radius zu seinem Umfang oder seiner Fläche. Die Größen haben ein irrationales Verhältnis zueinander und werden doch als Einheit (1) zur Gestalt (4).
Wollen wir das Verhältnis inhaltlich verstehen, so bedienen wir uns des voran dargestellten Wissens über die umfangreiche Würdigung des Archetyps der Zwei. Aus diesem Grunde werden wir hier nun nicht zuerst den sogenannten Einheitskreis (r = 1) betrachten, sondern uns zunächst dem Kreis mit dem Radius 2 zuwenden. Nach dem bereits Gesagtem verspricht er uns, Näheres über die Einheit zu verraten. Wir nennen den Kreis mit dem Radius 2 einen Gleichheitskreis, denn seine anderen zwei Größen, sein Umfang und seine Fläche haben die eine, gleiche Größe von 4 π. Die Gleichheit und Einheit zweier Kreisgrößen ergibt sich nun nicht nur bei einem Radius 2, sondern auch bei einem Kreis mit dem Umfang 2. Auch er zeigt ein Gemeinsames an, nämlich die Gleichheit von Radius und Fläche. Sie beträgt 1/π.
Der Kreis mit seiner aus nur einer einzigen Linie bestehenden Umfang zeigt uns in der denkbar einfachsten Gestalt, wie aus einer Linie eine Fläche wird. Er ist ein Archetyp und «erzählt», wie eine höhere Dimension sich aus einer niederen entwickelt. Die Gleichheitskreise (U = 2 oder r = 2) werden dabei noch konkreter. Sie offenbaren, dass es das Wesen der Zwei ist, das die Einheit und Ganzheit ansichtig macht!
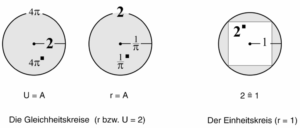
Abb. 4 Das Wesen der Zwei offenbart Einheit. Die «Gleichheitskreise» mit dem Umfang 2 oder dem Radius 2 führen zur Gleichheit und Einheit der anderen beiden Kreisparameter (A = U bzw. A = r). Gleiches «erzählt» auch der Einheitskreis über das von ihm umschlossene Quadrat 2 (rechts).
Hinweis zu weiterführenden Aufsätzen:
¹ Der Begriff der hier verwendete Begriff der «Ähnlichkeit» meint, «Einheit wird sichtbar“. Was der Begriff aussagt, das wird deutlich an seiner Herkunft. In Mittelhochdeutschen war das «ähnlich» noch «einlich». Die mit dem Begriff erfasste Einheit ist keine völlige Gleichheit im mathematischen Sinn von kongruent. Was einander ähnlich ist, das hat die gleiche Gestalt, erscheint aber in vielen anderen Dimensionen. Diese Einheit der Zahlen ist hier in der Epinomis gemeint.
Die „vierbeinige“ Eintagsfliege des ARISTOTELES von Michael Stelzner Inhaltsverzeichnis 1. Die Behauptung eines Phänomens und ihre Absicht Der große Denker ARISTOTELES lässt sich in seiner
Identität und Wahrhaftigkeit – der Kreis des Radius 2 und die Kugel des Radius 3 von Michael Stelzner Inhaltsverzeichnis 1. Mensch und Identität Identität hat
Die Bedeutung der Zahlen als das Verbindende von Wissenschaft und Mystik in Anknüpfung an die jüdisch-kabbalistische Tradition von Michael Stelzner Von der Wissenschaft zur Mystik
