Die Zahl Sechs und das «Sterben» von Jesus
Die Zahl Sechs und das «Sterben» von Jesus von Michael Stelzner Inhaltsverzeichnis 1. Vorbemerkung Über das Wesen des Archetyps der Sechs als auch über seine
Vom Wesen der Zahl
oder von der heiligen «Ordnung der Neun» zum Dezimalsystem
von Michael Stelzner
Das Wesen einer Wissenschaft ist das Erkennen von Mustern und Strukturen. Die dazu verwendeten Methoden und Systeme sind vielfältig. Am Ende aber laufen alle auf das Wesen der Zahl zu. Keine Wissenschaft kommt ohne die Zahl aus (s. Aufsatz „Warum die Zahlen zählen“). Die sich daraus ergebende Schlussfolgerung, dass Zahlen notwendig eine Qualität haben, wird dann jedoch zumeist mit dem Hinweis übergangen oder verworfen, dass es eine Vielzahl von unterschiedlicher Zählsystemen gibt. Ihre Existenz nährt den Zweifel daran, dass einer Zahl ein gleichbleibender Charakter zugeordnet werden kann.
So berechtigt der Zweifel auch scheint, so sicher erscheint auch die Quantentheorie, in der die Zahl die entscheidende, feste Größe ist, welche unausweichlich «neben» den unterschiedlichen Naturgrößen steht, deren Quanten (kleinste Größen) sie zählt. Die Zahlen sind existent! Was aber kann eine Größe alias Quantität haben, das keine Qualität alias Existenz hat? Der Glaube, die Zahl hätte keine Qualität geht auf das naturwissenschaftliche, zählende Verständnis von der Zahl zurück, das seinem Grunde nach ein streng lineares Verständnis ist, das dem Denken nicht erlaubt, die einst postulierten Grenzen zu überschreiten. Was das für die Mathematik und die mit ihr operierenden Naturwissenschaften bedeutet, das hat uns der Philosoph und Mathematiker KURT GÖDEL im Jahre 1931 mit dem von ihm begründeten Unvollständigkeitssatz gezeigt. GÖDEL bewies, dass jedes logische System Sätze enthalten muss, die wahr, aber niemals beweisbar sind. Entgegen dem einstigen Traum der Mathematiker ist die Mathematik unvollkommen und nicht in der Lage, aus sich selbst heraus ihre eigene Konsistenz zu beweisen. Die Mathematik ist die Gefangene ihrer Grenzen und diese Grenzen sind die der Linearität. Es ist die Vorstellung vom Kontinuum des Zahlenstrahls, der das Denken gefangen hält.
Will man die Konsequenzen aus dem o.g. Unvollständigkeitssatz ziehen und der Mathematik und den Wissenschaften im allgemeinen im Hinblick auf das Wesens der Zahlen gerecht werden, so muss man deren Linearität und Sukzessivität mit den in ihnen wirkenden Dimensionssprüngen zusammendenken.
Die Religionen haben sich dem Problem angenommen und versuchen, die jeweils herrschenden Linearitäten zu überwachsen, indem sie die höhere Dimension des Seins im Dasein der Dinge und Subjekte miterfassen. Dabei fliehen sie nicht vor der Wirklichkeit. Wie die Mathematiker und Physiker wissen sie, dass jegliche Ordnung an der Zahl hängt. Auch wenn ihre Argumente unterschiedliche sind, so weiß doch jeder ernsthafte Wissenschaftler, dass ohne Zahl keine Ordnung vorstellbar ist.
Die Zahlen sind die letzten bzw. ersten Entitäten und somit die Ur-Sprache der Natur. Aus diesem Grunde entspricht in heiligen Alphabeten jeder Buchstabe einer Zahl. Buchstaben sind Zahlen und umgekehrt. Schaut man genauer auf die Alphabete, so entdeckt man weiter ihre triadische Konstitution. Die in den Alphabeten eingefangene Ordnung bedient sich der linearen Abfolge des Zahlenstrahls, der auch die zählenden Naturwissenschaften folgen. Doch erfassen die Buchstaben alias Zahlen nicht nur den bekannten Wechsel von Dimensionen, wie er im Dezimalsystem beispielsweise nach der Zehn erkennbar ist. Die heilige Ordnung der Buchstaben erzählt vielmehr von einem allgegenwärtigen, prinzipiellen Wechsel der Dimensionen in Form einer universellen, fraktalen Struktur! Wir erblicken den Wechsel der Dimensionen bereits im Sprung von einer Zahl zur nächsten. Zwei Zahlen trennt jeweils ein archetypischer Bruch (2). So verkörpert die Zwei und Polarität in ihrem Unterscheidungspotential bereits eine völlig andere Dimension als die ihr vorausgehende Eins und Einheit. Jede weitere Zahl bringt eine neue Dimension hervor und erzählt von der ihr eigenen Qualität. Der von der einzelnen Zahl erzeugte Bruch führt über die so entstehende Linearität der Zahlen zu einer weiteren Dimension, die uns in Form der Zählsysteme erscheinen, denn die verschiedenen Zählsysteme legen verschiedene Längen von Linearitäten zugrunde. Auch Zählsysteme treten wiederum in eine lineare Beziehung. Sie führen zu einer neuen und höheren Linearität und einer neuen Dimension. Der durch ein bestimmtes Zählsystem veranschaulichte Bruch ist nicht allein die Erscheinung einer speziellen Linearität und Zählweise, sondern ein allgegenwärtiges Prinzip, das als solcher durchschaut werden will. Das macht die triadische Ordnung der Archetypen.
Die heilige Ordnung fängt die fortlaufenden, fraktalen Brüche als Ganzes ein. Dabei bedient sie sich der Zahlensprache in einer höheren Weise. Sie reflektiert, dass jede Dimension nur durch einen «Schlupf», eine gewisse Unvollkommenheit existiert und sie reflektiert auch, dass in jeder der Dimensionen eine jeweils noch unerkannte und höhere Dimension wirkt.¹ Was KURT GÖDEL mit seinem Unvollkommenheitssatz für die Mathematik formuliert hat, ist die Grundlage der heiligen Alphabete. Unter ihrem Blickwinkel erschließt sich deren Konstitution.
Die Tora wurde mit den 22 Buchstaben des hebräischen Alphabets verfasst und das basiert wiederum auf der Ordnung von neun Archetypen, die sich in wachsenden Dimensionen wiederholen (Abb. 1). Die zunächst ins Auge fallende Linearität ist jedoch keine profane, denn sie entsteht durch die Ordnung von Archetypen in der jeder Buchstabe einer Zahl entspricht. Die Identität von Buchstaben und Zahl erzählt vom Zusammenwirken zweier Dimensionen. Die Verbindungselemente der zwei Dimensionen sind die jedem Archetyp jeweils zugeordneten Bildsymbole. Jeder Archetyp wird so über drei Ebenen erfasst, (1) die Zahl, (2) den Buchstaben und (3) das ihm entsprechende Bildsymbol. Die triadische Schau sprengt die Vorstellung von einer profanen Linearität und öffnet sich der Erzählung der Zahl. Das derart konstituierte Alphabet enthält zwei Ordnungsstrukturen, die sich, wie wir noch sehen werden, auch in zwei Zahlenordnungen und zwei Zählsysteme niederschlagen.
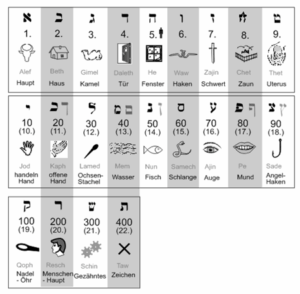

Abb. 1 Das hebräische Alphabet hat 22 Buchstaben. Es folgt der heiligen Ordnung der Zahl. Ihre Basis ist die 3 bzw. deren Quadrat (9 = 32). Die 22 Buchstaben bieten so einen dreifachen Erkenntniswert: Buchstabe, Zahl und Sinnbild
Zu den drei Erkenntniswerten des hebräischen Alphabets tritt mit dem Archetypus 10 ein neuer und vierter Erkenntniswert hinzu, der den Zahlenwert nochmals differenziert. Die 10 überschreitet die scheinbare Linearität der Neun und manifestiert eine neue Grundlage, aus der eine neue Ordnung mit einer neuen Linearität (10-90) erwächst. Die nun höhere Zahlenordnung ist die der differenzierten «Zahlenwerte». Sie wird sichtbar in den Zahlenwerten 10-90. Die abermals neue Unterscheidung von «Reihenwert» und «Zahlenwert» ermöglicht neue Erkenntnisse.
Waren Reihenwert und der Zahlenwert eines Buchstabens bis einschließlich der 10 noch identisch, so ändert sich das aufgrund des durch die 10 erzeugten Bruches. Obwohl die 10 den Bruch herbeiführt, sind bei ihr Reihenwert und der Zahlenwert noch eines. Erst der Archetyp 11, der zweite Wert der zweiten Dimension (10-90) macht die Differenzierung auch sichtbar. Sein Zahlenwert ist nicht 11 sondern 20. Die erschaute Unterscheidung von „gezähltem“ Buchstaben und dem ihn zugeordneten «erzählenden» Zahlenwert führt zu einem differenzierteren und höheren Blick auf das Wesen der Polarität und des Unterscheidens (2). Das erzählt der Wandel der 2 zur 20.
Die mit der Zehn grundgelegte, zweite und andere Dimension ist die «Bewusstseins-Dimension» (siehe die Bewusstseinsformel 10 = 5 + 5). Sie reflektiert über die vom Zählen abweichenden Zahlenwerten die bis dahin verborgen gebliebenen, doch gleichwohl immer schon vorhandenen und erzählten, inhaltlichen Werte!²
Die heilige Ordnung der Buchstaben und Zahlen macht insbesondere über ihre zweite Dimension (10-90) deutlich, dass es nicht nur ums «Zählen», sondern ums «Erzählen» von Werten geht. Die neuen, vom profanen Zählen abweichenden Zahlenwerte überwachsen das zählende Element der ersten, linear erscheinenden Dimension. Deren Prinzip aber wirkt weiterhin. Die Buchstaben alias Zahlen der zweiten Dimension folgen noch immer der einstigen Linearität des Zahlenstrahls. Doch manifestiert diese sich nun in Form von Sukzessivität, die neue und höhere Werte sichtbar macht. Sukzessivität ist mehr als Linearität, setzt aber die Erfahrung von Linearität voraus.
Die Sukzessivität überwächst die Vorstellung von der profanen Linearität. Aus der Perspektive der zweiten Dimension (II) erscheint die erste Dimension (I) unvollständig (s.o. KURT GÖDEL), weshalb sie dem «Verfehlenden» nun notwendig die fehlenden Werte hinzufügt. Doch fügt sie die (nur) ihrem Vermögen nach hinzu, das seinerseits ein beschränktes ist. Das den Dimensionen jeweils Fehlende verleiht nicht nur ihnen, sondern auch dem Gegensatz der Dimension zueinander (I ⇔ II) Konturen. Die ermöglichen der dritten Dimension (100-400) dann wiederum, die Widersacher zu verbinden – «zu einen». Die dritte Dimension berichtet von «einem» letzten zusammenfassenden Wert. Der besteht aus vier Zahlen (100 200 300 400). Die letzte und höchste von ihnen ist die zweifach erhöhte Vier (400). Das ihr zugeordnete Sinnbild ist das «Kreuz» oder «Zeichen». Es steht formal und inhaltlich für alles nach ihr Kommende.
Die Perspektiven auf die Reihenwerte oder die Zahlenwerte der Buchstaben eröffnen zwei Zählweisen. Sie illustrieren zwei formal voneinander unterschiedene Umgänge mit dem Anderen und Jenseitigem. Wer das Andere, das es den Gesetzen der Polarität zufolge immer gibt und demnach auch noch jenseits der Welt gibt, erschließen will, der kann das nur im Rahmen dessen, was seine Existenzbedingungen zulassen. Das zu Erschließende muss in seiner Welt, seiner Sprache und seinen Bildern einen Platz finden. Das bedeutet, dass das Jenseitige, das eigentlich nicht rational zu Erfassende – hier die Ganzheit als Hintergrund – dennoch auf eine rationale Weise eingeholt werden muss. Wir reden von einer Grenzsituation, die ähnlich einer Tür sowohl aus- als auch einschließt. An jener Tür, jener Grenze begegnen sich das Rationale und das Irrationale.
Was das Jenseitige, das «über-die-Welt-Hinausragende» in Wirklichkeit ist, das vermittelt die Tora in ihrem ersten Buch Genesis. Dort erklärt sie das Dasein mit Hilfe der Siebener-Ordnung. Sie zu verstehen ist notwendig, um auch die ihr folgenden Botschaften und ihre Zählordnungen zu verstehen. Die Genesis erhellt den Übergang von einem Zählsystem zu einem anderen. Auch wenn die Sieben hier nicht erklärt werden kann, so muss gegenwärtig doch der Kern ihres Wesens benannt werden: Die Sieben vermittelt, dass das jeweils „Darüber-Hinaus-Ragende“ weder Zufall noch Willkür ist, sondern von den Grenzen des existierenden, schauenden und handelnden Subjekts definiert wird.
Die in der Genesis vorgestellte Zahlenordnung ist eine triadische und sie schließt zunächst mit dem Zusammenfluss der ersten zwei Dreiheiten (Tage 1 2 3 und Tage 4 5 6) im Bild von der 7, dem «Tag der Gottheit» ab. Die besagte Grenze zwischen dem konkreten Dasein und dem ganzheitlichen Sein liegt in der Zahlenordnung der Genesis zwischen der 6 und der 7. Führt man die Ordnung im Wissen um die fraktale Wirkung der 3 fort, wie das im Bild von der «Flussform der Zahlen» der Fall ist, dann entsteht ein neues und größeres Muster, das eine neuen Linearität aufscheinen lässt. Seine Grenze ist nicht mehr die zwischen 6 und 7, sondern die zwischen 9 (= 32) und 10. Es ist das Muster des hebräischen Alphabets. In ihm ist das „Darüber-Hinaus-Ragende“ und „Jenseitige“ nun die 10. Sie symbolisiert die Einheit und Ganzheit und umfasst nach dem Vorbild der 7 alles ihr Vorangehende.
Die grundlegende Botschaft der Genesis ist die der 7. Sie erschließt sich über zwei Sichtweisen, die triadische und die lineare. Die der Sieben-Tage-Erzählung folgenden Texte entfalten die Botschaft und beschreiben ihre zwei Sichtweisen in Form zweier hierarchischer Zahlensysteme, in deren Zentrum nicht mehr die 6 und die 7, sondern nunmehr die 9 und die 10 stehen. War die Zahl der Genesis-Gottheit namens «Elohim» noch die 7, so entfaltet sich aus ihr über den Zwischenschritt «JHWH Elohim» die EINE für die Subjekte maßgebende Gottheit namens JHWH (Gen 4:1). Der geheimnisvolle, aus vier Buchstaben bestehende Gottesname JHWH (10-5-6-5) geht vom Wissen über die Zehnzahl aus und erschließt sich über sie. Das erzählen die späteren Texte von der Offenbarung des Namens, in dem sich die Tetraktys (1+2+3+4 = 10) und die Subjektformel (5+5 = 10) verbergen (siehe Ex 3:14 und Dekalog).
Das Wesen der neuen und maßgebende Gottheit JHWH besteht in der Verbindung zweier Dimensionen, der Dimension des konkreten Daseins und der des ganzheitlichen, göttlichen Seins. Ihnen entsprechend bedient sich auch die Sprache der Gottheit zweier Zähl- und Erzählsysteme, die durch ein über sie hinausgehendes Drittes verbunden sind. Das heilige Alphabet setzt diese Spannung und deren Erlösung durch das Zusammenwirken zweier Zahlensysteme ins Bild – das der 9 und das der 10.
Der Zaunpfahlfehler entsteht beim Abzählen eines aus Pfählen und Zwischenfeldern bestehenden (nicht ringförmig angeordneten) Zauns durch das Fehlen einer der Ganzheit angemessenen Unterscheidung. Beim Zaun handelt es sich um die Unterscheidung der Anzahl der Objekte und der Anzahl der Zwischenräume. Zählt man die Zwischenfelder, so zählt man in Wirklichkeit die Anzahl von Differenzen und Beziehungen. Da jedes Dasein generell durch eine Beziehung zustande kommt und so immer ein In-Beziehung-Sein ist, gilt das auch für den Rahmen des Zählens selbst, der das Zählen und Unterteilen erst möglich macht. Der Rahmen sind die „Pfeiler“.
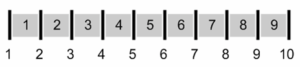
Abb. 2 Der Zaunpfahlfehler: Zwischen 10 Pfählen lassen sich nur 9 Felder platzieren
Zählen und Berechnen geschieht immer innerhalb einer bestehenden Linearität und die führt früher oder später zu einem Zaunpfahlfehler. Anders verhält es sich, wenn man beim Zählen und Berechnen aufmerksam die Ganzheit im Blick hat. Das ist beim Zählen der Zaunzwischenräume eines ringförmigen Zauns der Fall. Bei ihm fallen die grundlegenden Pole «Anfang und Ende» (im Extrem «Null und Unendlich») zusammen. Sie stehen für die alles umschließende Einheit und Ganzheit, die notwendigerweise nur über zwei polare Aspekte begriffen werden kann. Beim Anblick eines kreisförmigen Zauns erfasst das Bewusstsein über das Bild des Kreises das Ganze, das Teilhaftige und deren Zusammenwirken.
Das Bild vom Zaunpfahlfehler hilft uns, die Beziehung zwischen dem Neunersystems, das in der Flussform der Zahlen sichtbar wird und dem Zehnersystem mit dem wir praktisch umgehen, zu erfassen. Das Zehnersystem zählt die Pfeiler und schließt damit das Höhere, die Zehn als ein Da-Seiendes ein. Es zieht das an sich Höhere in die Linearität herunter. Das hat zwei Seiten. Zum einen ermöglicht es ein genaues Berechnen. Zum anderen engt es den Blick auf das Wesen des Höheren auch wieder ein. Das Zehnersystem „verdinglicht“ das abstrakte Sein und manifestiert damit einen „Fehler“ im Sinne des „verfehlten Bewusstseins“ über das Wesen der Einheit und Ganzheit. Das geschieht bei jedem linearlogischen Vorgehen und wir handeln im Profanen vorwiegend linearlogisch.
Der Zaunpfahlfehler illustriert die Wirkung einer triadischen Sichtweise. In Bezug auf zwei unterschiedliche, einander folgende Zählsysteme zeigt er uns, dass zwei lineare Perspektiven notwendig sind, um in der Beziehung ein größeres Ganze zu erschauen, das die zwei profanen Linearitäten überwächst. Er demonstriert aber auch, dass beide Zählsysteme, auch das fortentwickelte Zählsystem der 10 der «linearen Falle» anheimfallen können.
Das Zählsystem der 10 entsteht über eine Dehnung des 9er-Systems. Der konkrete Vergleich der beiden lenkt die Aufmerksamkeit auf die begrenzenden Endpunkte (unterhalb von 1 und oberhalb von 9). Im «niederen» 9er-System finden sie wenig oder keine Beachtung. Erst mit seiner Dehnung alias Bewusstseinserweiterung erscheinen sie als «begrenzende Pfosten» und werden vom neuen und erweiterten 10er-System integriert. Die Null und die Zehn werden zum Bestand des Zehnersystems. Dabei wird der Wert der Null in aller Regel nur «nach oben hin» in Form der Zehn wahrgenommen. Der gleichzeitige Aus- und Einschluss der Null ist der Preis der Polarität.
Das neue Zählsystem erfordert Achtsamkeit, denn es birgt in seinem Erheben nach wie vor die Gefahr der Bindung an eine lineare Logik. Konkret: Das gewonnene Rechen und Zählen darf nicht dazu führen, den Zahlen alias Archetypen ihre Existenz absprechen zu wollen, denn aus ihnen heraus existieren sie.
Das Wissen um die Existenz von (Zahlen-) Archetypen ist die Voraussetzung, das Wesen einer Zählweise und deren Unterschiede zu erfassen. Die Art der Zählung ist die Art der Erzählung. Das 9er-System erzählt uns über das triadische Muster von den im wörtlichen Sinn zu verstehenden Wirklichkeiten der Archetypen. Das ihm folgende 10er-System manifestiert (4) sich aus ihm heraus und bildet die Grundlage für unserer Sicht auf die Welt.
Das 9er-System erfasst das Ganze aus der Perspektive des wirkenden Geistes und somit aus der Perspektive der Drei. Das 10er-System hingegen erfasst das Ganze aus der Perspektive der Manifestationen, der Dinge und der Substanzen und somit aus der Perspektive der Vier.
Das sich über diese Dualität der Muster erhebende Bewusstsein (5) benötigt für sein Erheben beide Erzählungen. Es führt sie im übergeordneten, pythagoreischen Muster³ zu einer neuen Einheit zusammen. Die nachfolgenden zwei Tabellen stellen die Charaktere beider Zähl- und Erzählweisen noch einmal gegenüber.
Das 9er-System Die heilige, triadische Ordnung der Zahlen
|
1 2 3 4 5 6 7 8 9 ➔ 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27
Die neue Dimension beginnt mit 10.
|
Die heilige Zählweise basiert auf der Triade. Sie thematisiert vor allem die Grenze zwischen zwei Dimensionen. Das Neunersystem öffnet die der Siebenzahl scheinbar noch anhaftende Grenze und öffnet sie zum Bild einer fortlaufenden Flussform. Sie schließt ihrem Prinzip nach alle Zählsysteme ein! Denn: Sie eröffnet die Spannung zwischen den Dimensionen vom Begrenzten und Unbegrenztem immer aufs Neue. Das fordert das Bewusstsein des Individuums (5) heraus, dessen Aufgabe ist es, die Gegensätze auf rechte Weise miteinander zu verbinden. Das führt endlich zu einer neuen und erweiterten Zählweise – dem 10er-Systems. Es findet seinen Niederschlag im Dekalog (10 Geboten) und illustriert das Wesen des BEWUSSTSEINs
|
Das 10er-System Die (höher)lineare und somit auch profane Ordnung der Zahlen.
|
0 1 2 3 4 5 6 7 8 9 10 ➔ 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30
Die neue „Dimension“ beginnt mit 11. |
Das Dezimalsystem nimmt das einst Jenseitige (10) in einer neuen Natürlichkeit (4) in sich auf. Insofern handelt es sich um eine neue, profane Zählweise, denn der Zehn wird innerhalb der noch ersten Dimension ein Wert zugeordnet. Das Profane obsiegt, wenn mit dem Jenseitigen formell-regelhaft, d.h. nur zählend anstatt auch erzählend und bewusst umgegangen wird. Mit der gewonnenen Effektivität gewinnt auch die Willkür an Macht: Zufall und Schicksal. Sie lassen nur sehr schwer oder gar keinen inhaltlichen Bezug mehr zum erlebenden Subjekt erkennen.
|
Eine «heilige Schrift» umfasst mehrere Bewusstseinsdimensionen. Ihre Buchstaben zählen und erzählen über die Dimensionen hinweg von der in der Vielheit stets durchscheinende und regieführenden Einheit.
Selbst die rechnende, weil «zählende» Mathematik lebt von der sie überragenden Einheit Ganzheit und Vollkommenheit, die sich in ihrer einfachsten Weise in der Triade kundtut. Die Mathematik bedient sich ihrer gern, ohne sich darüber bewusst zu sein. Ein Beispiel ist der Gebrauch der Quersummenbildung, die seit jeher in der «Zahlenkunst» verankert ist. Dort ist sie u.a. unter dem Begriff der theosophischen Addition bekannt und hilft, die Einheit auch über die Dimensionen hinweg zu erfassen. Die Quersumme macht die in der einfachen und begrenzten Zahlenreihe nicht unmittelbar sichtbaren inhaltlichen Zusammenhänge erkennbar.
Das Verfahren wird im Profanen wie im Heiligen geschätzt. Die Mathematik nutzt die Quersumme beispielsweise in Form der schnellen Teilbarkeitsregel für die Zahlen 3 und 9. Der auf die Zahlenqualitäten orientierte Umgang findet in der fortlaufenden Quersummenbildung ein Mittel, um mehrstellige Zahlen auf nur eine Zahl und somit auf eine der Grundqualitäten von Eins bis Neun zurückzuführen. Die Zusammenhänge sind leicht ersichtlich, denn im Neunersystem sind alle Zahlen einer Senkrechten über die gleiche Quersumme verbunden.
Das 9er-System trennt deutlich das Diesseitige vom Jenseitigen und fördert dabei über das notwendig entstehende Dritte die Herausbildung des Bewusstseins. Das Bewusstsein wird erfüllt, wenn es vom Wesen der Vier, alias dem Logos erreicht wird und das Subjekt als Individuum (das Ungeteilte) „durch das Kreuz hindurch“ (4) die Einheit (1) offenbart. Die Religionen und Mythen des Abendlandes beschreiben solche erlösten Bewusstseinszustände, an herausragenden Figuren, wie Henoch, Moses oder Christus. Ihr gemeinsames Merkmal ist die Überwindung der Vorstellung vom absoluten Ende, d.h. vom Prinzip des Todes bzw. des Grabes.
Die Bedeutung der 10 und des Dezimalsystems lässt sich in seiner Tiefe erst über die Ordnung der Neun verstehen. Was sich in neun Archetypen dem Bewusstsein kundtut, das manifestiert (4) sich in Gestalt der 10. Das schauende Subjekt erkennt, dass die Zehn eine erhobene, d.h. eine mit Dimension erfüllte Eins alias Einheit und Ganzheit ist. Der Weg des Erkennens führt über die neun Archetypen, deren Ursprung wiederum die Triade ist, denn sie bringt die Neun durch ihren Selbstbezug hervor (32). Am Ende geht es um nichts anderes als um das Erkennen des wahren Wesens der Einheit (1), der Polarität (2) und der wahrhaftigen Funktion (3). Das meint Platon, wenn er in der Mitte seines Hauptwerkes, der Politeia schreibt:
„ … was allen Künsten und Forschungen und Wissenschaften unentbehrlich ist, und was denn jeder mit als Erstes erlernen muss. Diese ganz bescheidene Weisheit: die richtige Kenntnis der Eins, der Zwei und der Drei.“⁴ Dass unter der »richtigen« Kenntnis nicht nur eine quantitative sondern vor allem auch eine der übergeordneten Idee zugehörige qualitative Schau zu verstehen ist, die sowohl dem Kriegsmann wie dem Philosophen dient, das stellt Platon klar und deutlich heraus: „Es obliegt uns also dies Fach (Zahlenkunst) zum gesetzlichen Lehrfach zu machen und diejenigen, die künftig im Staate der höchsten Amtsgewalt teilhaftig sein sollen, zu veranlassen sich der Zahlenkunst zuzuwenden und sich mit ihr zu befassen nicht etwa bloß in laienhafter Weise, sondern bis sie durch reine Vernunfttätigkeit zur Anschauung der wahren Natur der Zahlen gelangt sind, eine Art der Behandlung, die nichts gemein hat mit Kaufen und Verkaufen wie bei Kaufleuten und Krämern…“. Für Platon war jenes Lehrfach ein „besonders feines Fach“, weil es, wie er es ausdrückte, „die Seele offenbar nötigt auf dem Wege des reinen Denkens sich der reinen Wahrheit zu nähern.“⁵
Mit dem erworbenen Wissen über die Muster der Ordnung kann man die Frage nach dem Wesen der Zahlen genauer beantworten. Da sie die letzten bzw. ersten Entitäten und somit die Ur-Sprache der Natur sind, bedarf es, um sie zu erfassen, eines abstrakten Denkens. Nach den vorangehenden Beschreibungen möchte ich die Frage, was eine Zahl ist, hier nun noch einmal und noch abstrakter, also so kurz wie mir möglich, beantworten:
Die Zahl ist die reinste und vollkommenste Manifestation der Triade – der Drei-Einheit. Zahlen existieren und leben von drei Eigenschaften, von
(1) ihrer Einheit alias Ganzheit,
(2) ihrer Linearität alias Sukzessivität und
(3) dem fortlaufenden Dimensionswechsel.
Zu (1): Eine Zahl allein ist nicht vorstellbar. Zahlen verkörpern eine Vielheit, in der jedes Teil das «eine Ganze» (1) zur Anschauung bringt. Jede Zahl ist, weil sie ihre Existenz in ihrem Verhältnis zur EINS begründet! Ihre Rückbindung an das Ganze ist vollkommen und unauflösbar: So ist die Sieben beispielsweise eine Sieben, weil sie siebenmal die Eins ist.
Zu (2): Jede Zahl ist die Fortentwicklung einer jeweils vorangehenden Zahl. Ihr gemeinsamer Ursprung ist endlich die EINS. Die EINS alias die Einheit prägt zudem das Wesen der Differenzierung (2). Die EINS ist Urgrund und Differenzierungsgrund zugleich. So entwickelt sich beispielsweise die Sieben aus der 6 durch das Hinzufügen der EINS.
Zu (3): Das Hervortreten einer Zahl erzählt vom Hervortreten einer neuen Dimension, in der die vorangehende Dimension weiterwirkt. Die neue Dimension ermöglicht einen neuen und anderen Blick auf die Einheit und Ganzheit. Über das Wesen der zweiten Dimension, d.h. über das Unterscheiden entsteht ein zweiter, erweiterter Blick auf die Einheit und Ganzheit. Dieses Erbe der Sukzessivität manifestiert sich in einem fortlaufenden, hierarchisch geordneten Wechsel der Dimensionen.
Das Bewusstsein (5) erschaut die Zahlen und kann im Erlangen von Freiheit das gliedernde Maß für die Sukzessivität der Dimensionen wählen. So bilden sich die unterschiedlichen Zählsysteme heraus, wie beispielsweise das Neuner- und/oder das Dezimalsystem usw.
Die Flussform der Zahlen überwächst die unterschiedlichen Zählsysteme. Am Ende erklärt sich jedes Zählsystem über die Triade. Sie unterhält alle Existenzen und sie hat in allen Zählsystemen Relevanz. Nur die Erscheinungen der Triade unterscheiden sich. Kein Zählsystem kann die Triade hintergehen. Das gilt auch für das Binärsystem, das durch die Dualität von „Ja“ (1) oder „Nein“ (2) geprägt wird. Auch das Binärsystem bedarf eines Dritten, auf das sich die zwei Wahlmöglichkeiten beziehen. Das ist der Fluss (3)! Das Binärsystem berichtet, ob ein Fluss (3) vorhanden ist (1) oder eben nicht (2). Der Fluss ist das primär Wirkende. Sein Bejahen oder Verneinen ist sekundärer Art, auch wenn es für das unterschiedliche Erscheinen vor unserem Auge verantwortlich ist.
Obwohl es die verschiedensten Zählsysteme gibt, ist immer die Zahl die Determinante. Jede Zahl kann zweierlei. Sie hat eine einmalige, in der Form nur ihr zukommende Qualität und steht dennoch mit der Vielzahl aller anderen in einer definierten Beziehung, sodass man von der einen auf die anderen schließen kann. Sie ist das Ur-Beispiel der Einheit in der Vielheit, der letzten und höchsten Formel.
Die Zahlen repräsentieren Archetypen und haben als solche ein duales Wesen, das sich uns in zwei Zahlenordnungen zeigt. Die eine ist die profane Zahlenordnung, wie wir sie in Form des 10er-Systems täglich gebrauchen. Die andere ist die heilige Zahlordnung des 9er-Systems, auf der die hebräische Schrift aufbaut und über die sich das Wesen von Philosophie und Religion erschließt.
Fußnoten
¹ Die der linearen Ordnung folgenden Naturwissenschaften begegnen der höhere Dimension – die sie bewusst ausschließen – im Phänomen der Emergenz. Da sie ihr unverstanden bleibt, ordnen sie die Emergenz der Willkür und dem Zufall zu.
Bis zum Beweis von KURT GÖDEL haben die sich im System von zählenden Zahlen bewegenden Mathematiker nicht an die Existenz einer prinzipiellen Unbeweisbarkeit geglaubt. KURT GÖDEL hat das wahre Wesen der Polarität über ihren Selbstbezug (siehe Quadrat / die Polarität der Polarität / 22) zur Anschauung gebracht und bewiesen, dass eine prinzipielle Unbeweisbarkeit objektiv, d.h. aus einer Linearität heraus gesehen existiert.
² Mit der Zehnzahl alias dem «Zehnwort», «Dekalog» oder den «Zehn Geboten» beginnt eine neue Sicht auf die jüdische Gottheit JHWH. Sie beginnt mit der Erzählung vom «brennenden Dornbusch» und der Offenbarung des Gottesnamen JHWH (10-5-6-5 = 10 à 5 + 5 / Ex 3). Die bis dahin vor allem thematisierte Vierheit erreicht über die Tetraktys (1+2+3+4 = 10) nun vollends die Dimension des Bewusstseins (5).
³ Das pythagoreische Dreieck erfasst die Linearitäten 3, 4 und 5 im Bild der höheren Dimension, der Dimension der Fläche. Es macht anschaulich, wie das Bewusstsein (5) den in allem wirkenden Geist (3) mit der konkreten Substanz der Dinge (4) als eine Einheit (1) sehen kann. Solche Schau manifestiert die neue Dimension, die im pythagoreischen Dreieck in Form von 6 sichtbar wird.
⁴ Plato, Sämtliche Dialoge, Band IV, Der Staat, übers. und hrsg. von Otto Apelt, Felix Meiner Verlag, Leipzig 1923, Siebtes Buch, 522 St.
⁵ Plato, Sämtliche Dialoge, Band IV, Der Staat, übers. und hrsg. von Otto Apelt, Felix Meiner Verlag, Leipzig 1923, Siebtes Buch, 525St.
Die Zahl Sechs und das «Sterben» von Jesus von Michael Stelzner Inhaltsverzeichnis 1. Vorbemerkung Über das Wesen des Archetyps der Sechs als auch über seine
Die 2 und ihr Quadrat von Michael Stelzner Die Welt der Erscheinungen beruht auf der Polarität. Durch Reflexion bringt die Polarität „die Polarität der Polarität“
Der Mensch – das zweifach polare Wesen Die Zahl 390 von Michael Stelzner 1. Die Konstitution des Menschen Der Mensch ist „männlich und weiblich“ und