Suche

Was diese Zahl erzählt:

Was diese Zahl erzählt:

Das «Additionsgesetz 1- 4» alias das «Gesetz der Identität» im Lichte der Sechs

von Michael Stelzner

Inhaltsverzeichnis

1. Der Aufsatz, der eine Lücke schließen soll

Anderenorts habe ich das „Gesetz der Vier“ als ein „Additionsgesetz“ und das „Gesetz der Identität“ beschrieben. Da dies primär im Rahmen der Vorstellung des Wesens der Vierzahl erfolgte, konnte ihr Einfluss auf das Wirken der später beschriebenen Sechs nicht angemessen berücksichtigt werden. Andererseits ist das Wirkspektrum der Sechs universell und wiederum zu übergroß, um bei ihrer Beschreibung auch noch die Wechselwirkung mit der Vier erörtern zu können. Den Mangel möchte ich hier ausgleichen und die beide Zahlen in ihren unauflöslichen Zusammenhängen beschreiben. 

2. Der Würfel, ein Symbol für die Substanz (4) und für deren lebendige Funktion (6)

Es ist der Würfel mit seinen 6 Oberflächen und der Kantenlänge 6, der die Gleichheit von Innen und Außen sichtbar macht. Das Maß seiner Oberfläche ist gleich das seines Volumens (A = V). Warum das gerade bei ihm der Fall ist, das erklärt das Prinzip der Wahrhaftigkeit, das auf Identität beruht. Das Gesetz der Identität tritt in der Abfolge der Archetypen schon vor der Zahl 6 auf. Die Zahl Vier und das Quadratische erzählen von ihm. Aus ihr lassen sich alle weiteren Zusammenhänge ableiten und erklären. Der Würfel ist sodann der dreidimensionale Ausdruck des Gesetzes. 

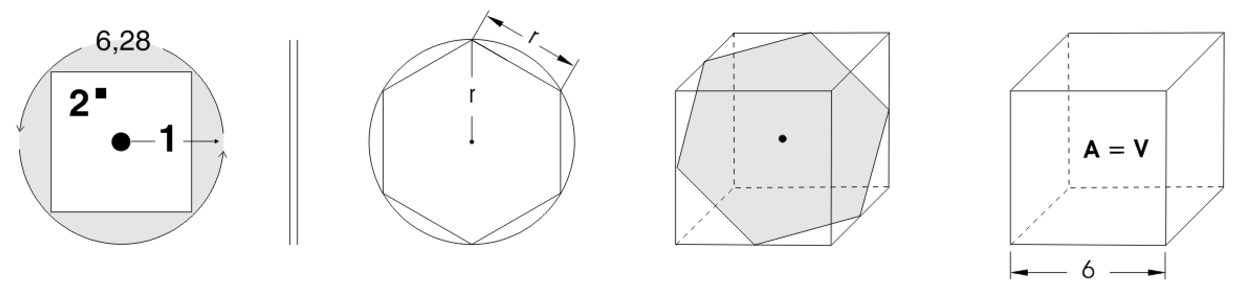
Abb. 1x  Durch die Zahl Sechs manifestiert sich Wahrhaftigkeit („wie innen, so auch außen“).

Die Basis ihres Erscheinens ist der Einheitskreis, der das Quadrat der Fläche 2 einschließt und das Andere (2) als ein von der Einheit Umschlossenes ansichtig macht. 

3. Das Gesetz der Vier in der Geometrie und in der Flussform der Zahlen

Anderenorts habe ich den Ur-Zusammenhang 1—4 das universelle Additionsgeschehen genannt. Einmal hervorgetreten wird es zur fortlaufenden Dynamik (3) und erscheint im Bewusstsein (5) der Subjekte wie ein Wunder (6). Analog einer Wunde klaffen die Gegensätze zunächst auseinander, können dann jedoch durch das Wesen der Sechs geschlossen werden (siehe pythagoreisches Dreieck der Seitenlängen 3, 4 und 5). Das Getrennte (2) das als ein gemeinsames Ganzes (1) erscheint ist jedoch älter als das Bewusstsein, denn das Gesetz ist die Geburtsbedingung aller Existenzen. Wir begegnen ihm bereits im Gleichnis vom Einheitskreis: Der Einheitskreis umschließt ein Quadrat der Fläche 2 (s. Abb. 2x). Was hier die Geometrie sichtbar macht, das erzählt auch die „Flussform der Zahlen“. Sie erzählt, dass jede der Eins sukzessiv entspringende Emanation in ihrer Weise ein Zeuge der Einheit ist. Vor allem aber erzählt sie – wie auch der Einheitskreis – vom besonderen Verhältnis der das Quadrat hervorbringenden Vier zur Einheit und Ganzheit (1). 

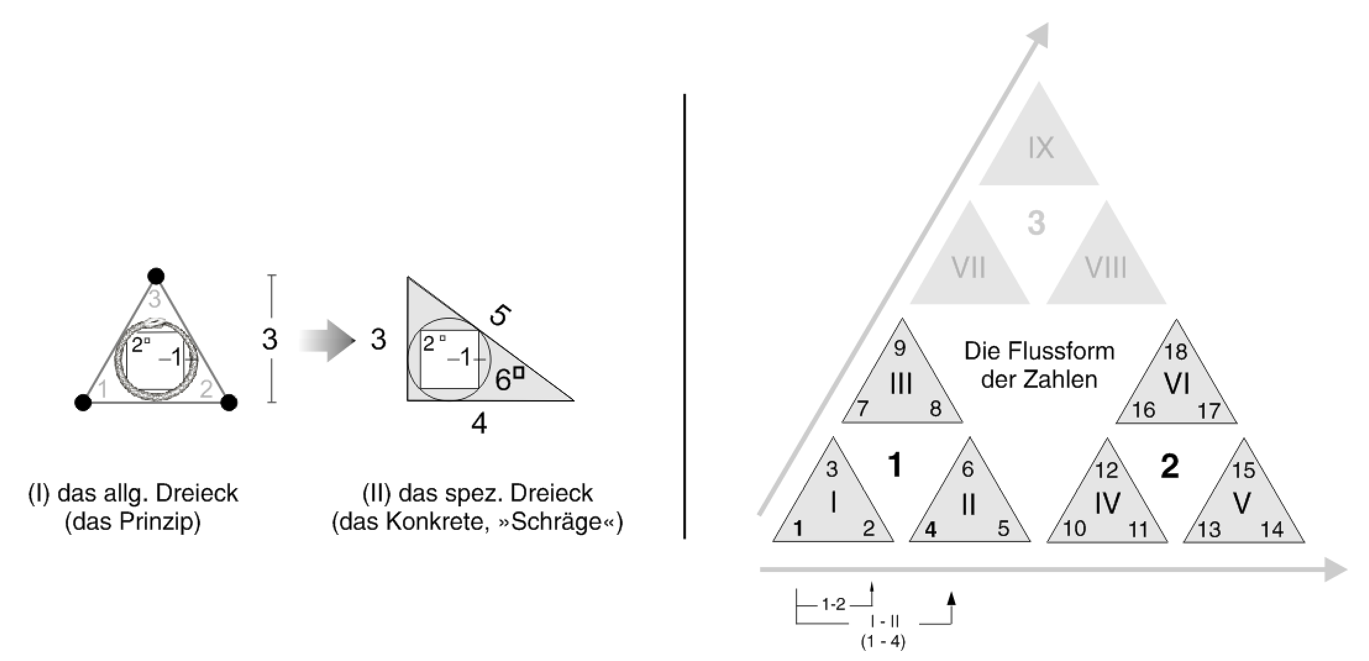
Abb. 2x  Wie der Einheitskreis (r = 1) über das vom ihm eingeschlossene Quadrat (A = 2) die erste mögliche Beziehung 1-2 zur Beziehung 1—4 expandiert und im Quadrat manifestiert, so zeigt auch die Flussform der Zahlen, dass die Beziehung 1—4 (I-II) eine Vergrößerung der Beziehung 1-2 ist. 

Sowohl im Einheitskreis als auch in den triadisch geordneten ersten vier Zahlen leuchtet die Einheit, Ganzheit und Vollkommenheit (1) noch auf. In ihrem Fortgang entzieht sie sich unserem fleischlichen Auge mehr und mehr, ist aber gleichwohl stets vorhanden. Das bringt eine neue und fruchtbare Spannung hervor, die das schauende Subjekt (5) dynamisiert (6) und auf neue Weise herausfordert.

Die so entstehende Dynamik ist die der Sechs. Sie entspringt ihrem Grunde nach dem Wesen der Drei, hat aber nun zwei Seiten, eine abwärts gerichtete und eine aufwärts gerichtete die nach dem Überwachsen der augenscheinlichen Formen und ihren scheinbaren Linearitäten (1—2) streben. Der Schritt verlangt die Aktivität des Subjekts, dem auch die neue Polarität in linearer Form erscheint, und etwas „Schräges“ (siehe pythagoreisches Dreieck) mit sich bringt. In Wirklichkeit ist die dem Subjekt erscheinende, neue Polarität von vertikaler Natur und mündet in die Sechs. Die verlangt dem Subjekt die Unterscheidung der Dimensionen ab.

4. Die biblische Zahlsymbolik und das Zuordnen der hebräischen Buchstaben zu Zahlenwerten

Wie man die Existenz von Dimensionen auch über die linear geordneten Zahlen zum Ausdruck bringt, das zeigt das Stellenwertsystem unserer Zahlenordnung. Doch es täuscht in zweifacher Hinsicht. Zum einen ist es nach wie vor ein lineares System, das die höhere Dimension notwendig in die niedere Dimension herunterbricht. Zum anderen erfasst das Kennzeichnen des Stellenwertes noch nicht wirklich die wahre Qualität der höheren Dimension. Die Zahl 12 soll das verdeutlichen: Die Zahl 12 steht für die „hierarchische Ordnung der Dinge“, denn sie ordnet die Archetypen 1 und 2 in einer linearen und doch erkennbar hierarchischen Weise so an, dass die Vorherrschaft und Höherwertigkeit der Einheit und Ganzheit (1) erkennbar ist. Weil in der 12 die beiden ersten Archetypen als ein harmonisches Ganzes auftreten, wurde sie zur Zahl der Ordnung.

So perfekt dieses System erscheint, so sehr verlockt es, die an sich triadische Ordnung der Archetypen doch wieder auf lineare Weise fortzuführen. Tatsächlich machen wir das regelmäßig im Umgang mit den Zahlen und verkennen dabei die den Archetypen eingeschriebene triadische Ordnung (PopUp-Fenster). Warum die Unterscheidung aber notwendig ist, das ersehen wir, wenn wir den Vorgang wie folgt geometrisch betrachten:

Schreibt man die Zahlen 1 und 2 – wie im Dreieck ersichtlich – nebeneinander, wird noch nicht deren wahre Unterscheidung, d.h. der inhaltliche Bruch zwischen den Archetypen 1 und 2 deutlich. Die Unterscheidung bleibt vage. Deutlicher wird der Bruch im Falle des vom Einheitskreis umschlossenen Quadrats der Fläche 2. Der Blick in die Geometrie lässt keinen Zweifel an der Unterscheidung der Dimensionen, die über die 1 und die 2 in Form von Kreis und Quadrat ins Bild gesetzt wird. Betrachtet man hingegen die scheinbaren Gegenpole 1—2 räumlich neben einander stehend, so könnte man die 2 im Raum auch anders anordnen und über eine Vielzahl von Punkten auf einem Kreisbogen platzieren. Auf diese Weise entsteht der Kreisumfang (PopUpFenster) im Kreisgleichnis.

Das Beispiel zeigt, dass die Anordnung der 1 und der 2 in der Zahl 12 das Prinzip Ordnung ausdrückt aber dennoch unvollkommen bleibt. Deutlich wird das beim Hinzutreten des 3ten Archetyps. Würde man ihn einfach an die 12 linear anfügen, würde die Zahl 123 entstehen und die mit der Drei einhergehende, erhebende Dimension untergehen. Die 123 bildet die dritte Dimension nicht ab. Sie führt nur die Stellenwertdarstellung fort und ist deshalb nur eine Variation innerhalb der 2ten Dimension.

Die biblische Zahlsymbolik löst das Problem, indem sie nur den ersten 9 (3×3) Archetypen alias Buchstaben auch den fortlaufenden Zahlenwert zuordnet, der jeweils der Zahl selbst entspricht. Die nächsten 9 Archetypen (10-18) erhalten hingegen die Zahlenwerte 10 20 30 40 50 60 70 80 und 90. Die dritte Reihe der Archetypen erhält entsprechend die Zahlenwerte 100 200 300 und 400.

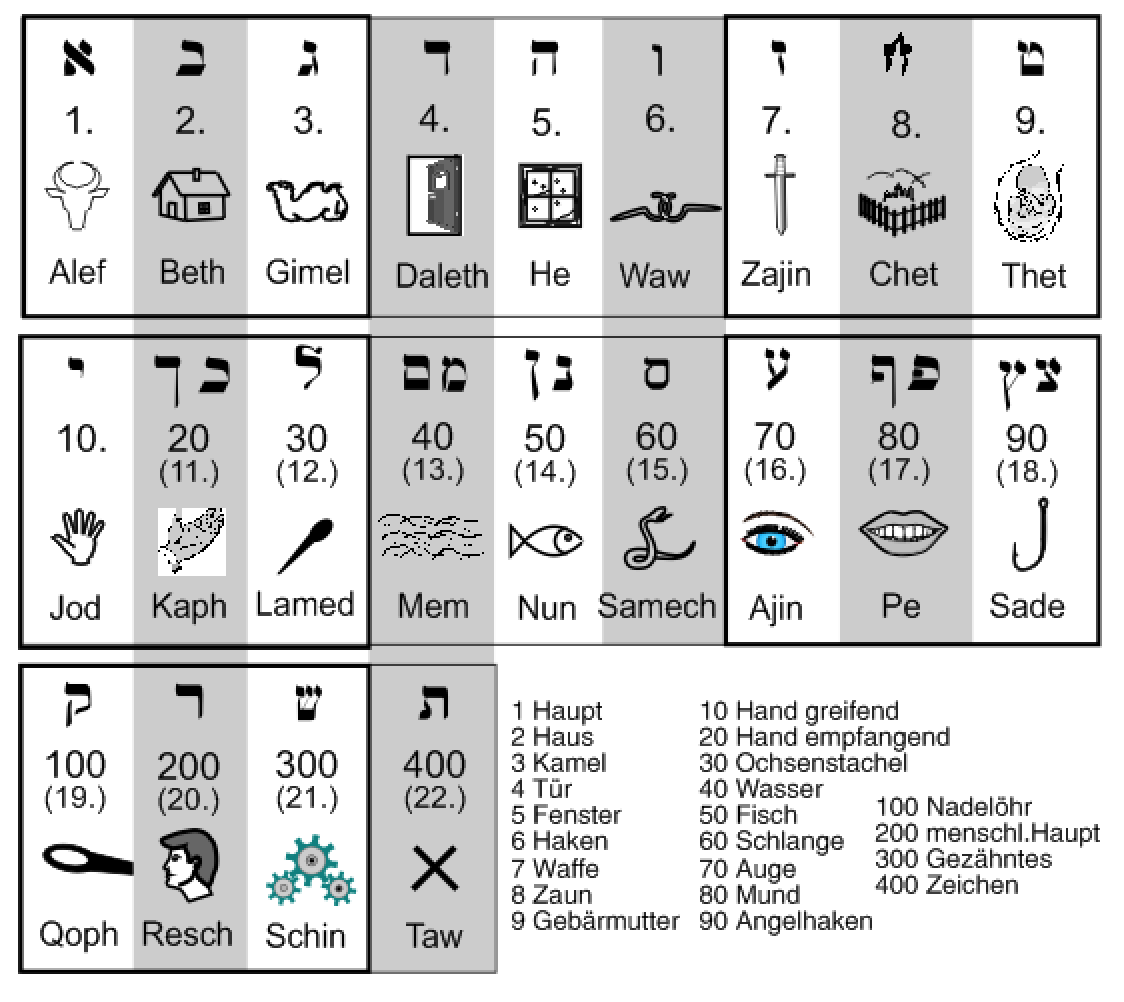
Abb. Die 22 hebräischen Buchstaben und ihre Zahlenwerte

Die Zahlenordnung der hebräischen Buchstaben hat eine triadische und zugleich abstrakt fraktale Struktur. Die so gewählte Struktur soll den Verfall in die Linearität bei der Interpretation der heiligen Texte verhindern. Die biblischen Texte vermeiden den Widerspruch nicht, sondern leben von ihm. In jedem verbirgt sich vielmehr die Botschaft eines höheren Seins, die den Leser über das Wesen der Drei zur Unterscheidung der jeweils vorliegenden Dimension führt.

Nach dem o.g. Beispiel wird dem Leser das Wesen der zweiten Dimension zwar über die 12 (1-2), die Zahl der Ordnung vermittelt, nicht jedoch die der dritten Dimension in der Zahl 123. Das geschieht über die Zahlenfolge 1-2-30, in der die Erhöhung der Drei (PopUp-Fenster) sichtbar wird. Auch kommt deshalb die Zahlen- bzw. Buchstabenfolge 1-2-3 in der gesamten Schrift nicht vor. Sie widerspricht der Ordnung der Dinge. Die Zahlenfolge 1-2-30 bedeutet „Gewissheit“. Obwohl die Zahlenfolge 1-2-3 nicht existiert, finden wir wohl die 123 als Zahlensumme eines Wortes. In dem Falle trägt das Wort beispielsweise die Bedeutung von „Schlachtordnung“. Das ist konsequent, denn auch die dreistellige Archetypenfolge 123 erzählt faktisch von der Drei und somit vom Prinzip der „Funktion“ und „Handlung“. Doch drückt sie nicht das verbindende und verbindliche Handeln aus, sondern das auseinanderwerfende, anstatt das zusammenführende Handeln.

Wie die Flussform der Zahlen in jedem der einzelnen Archetypen von seiner Beziehung zur Einheit, Ganzheit und Vollkommenheit (1) erzählt, so erzählen auch die 22 Buchstaben des hebräischen Alphabets auf ihre Weise von der an allem Anfang stehenden einen Gottheit. Jeder Buchstabe ist für sich eine Manifestation und somit eine prinzipielle Vierheit. In jedem Buchstaben wird dennoch ein Unterschiedenes (2) zu ihr thematisiert. Da die Unterscheidung (2) endlich aber immer das höhere Ganze (1) in seiner zweifachen Funktion (2 x 3) sichtbar macht, wirkt in jedem Buchstaben der Archetyp der Zahl 6. Der 6. Buchstabe, das „waw“ ( w ) bedeutet „und“. Er wird durch einen Haken symbolisiert. Mit anderen Worten: Jeder Buchstabe ist ein Verbindendes und Verbindliches, so wie die Sechs mit ihrer Bindungskraft die „Gangart der Evolution“ beschreibt.

Die hier vorgestellten Zusammenhänge lassen den Archetyp der Sechs als einen Endpunkt in der konkreten Welt erkennen. Die der Sechs folgende Sieben symbolisiert bereits ein Jenseitiges, das seinerseits wieder in die Welt hineinwirkt. Doch auch das wirkt wieder über die Sechs in sie hinein.

Fußnoten

¹ Die Zahlenfolge 1-2-30 bedeutet „gewiss sein“ oder auch „Gewissheit“. Als Ausdruck des erhöhten Dritten wertet sie aber nicht, um welche Art Gewissheit es sich handelt. So bedeutet die Zahlenfolge auch „Trauer“. Auch die Trauer bringt Gewissheit zur Anschauung, die Gewissheit des Todes und all seiner Folgen.

Weitere Beiträge

Datenschutz | Impressum | Kontakt